利用神经网络模型以及数据科学优化抽油杆泵性能与故障预测

2024-06-01

1.论文题目：自动识别抽油杆泵系统工作状态的方法：基于示功图的迁移学习和支持向量机#

Local image

摘要#

本论文提出了一种基于AlexNet的迁移学习和支持向量机（SVM）的自动故障诊断方法，用于识别抽油杆泵系统的工作状态。通过传感器采集的大量示功图数据，采用AlexNet提取代表性特征，并利用基于错误校正输出码（ECOC）模型的SVM进行分类。实验结果表明，该方法能有效减少人工劳动，提高识别准确率。

关键词#

工作状态识别，抽油杆泵系统，示功图，卷积神经网络，迁移学习，支持向量机

方法论详细介绍#

方法论概述#

该方法论由两个主要部分组成：自动特征提取和故障分类。具体步骤如下：

卷积神经网络（CNN）和迁移学习：采用AlexNet网络从示功图中自动提取有代表性的特征。AlexNet网络由八层组成，包括五个卷积层和三个全连接层。
支持向量机（SVM）：利用ECOC模型的SVM进行多类分类。ECOC模型将多类问题转化为多个二分类问题，采用冗余的错误校正码来减少分类误差。

数学公式#

SVM优化问题#

目标是找到分离超平面，定义为：

$\omega^T x_k + b = 0$ 其中， $\omega$ 是权重向量， $b$ 是偏置项。

约束条件为：

$y_k (\omega^T x_k + b) \geq 1 - \xi_k, \quad \xi_k \geq 0$

目标函数为：

$\min_{\omega, \xi} \left( \frac{1}{2} \|\omega\|^2 + C \sum_{k=1}^{N} \xi_k \right)$

ECOC编码设计#

对于多类问题，使用one-versus-one编码设计，每个类有一个长度为28的编码。编码设计如下表所示：

Class	Code Word
0	1 -1 0 0 0 0 0 0
1	0 1 -1 0 0 0 0 0
2	0 0 1 -1 0 0 0 0
3	0 0 0 1 -1 0 0 0
4	0 0 0 0 1 -1 0 0
5	0 0 0 0 0 1 -1 0
6	0 0 0 0 0 0 1 -1
7	0 0 0 0 0 0 0 1

代码示例#

下面是使用Keras库实现AlexNet的示例代码：

from keras.models import Sequentialfrom keras.layers import Conv2D, MaxPooling2D, Flatten, Dense, Dropoutfrom keras.optimizers import Adam
# 定义AlexNet模型
model = Sequential([
    Conv2D(96, (11, 11), strides=(4, 4), activation='relu', input_shape=(227, 227, 3)),
    MaxPooling2D(pool_size=(3, 3), strides=(2, 2)),
    Conv2D(256, (5, 5), activation='relu', padding='same'),
    MaxPooling2D(pool_size=(3, 3), strides=(2, 2)),
    Conv2D(384, (3, 3), activation='relu', padding='same'),
    Conv2D(384, (3, 3), activation='relu', padding='same'),
    Conv2D(256, (3, 3), activation='relu', padding='same'),
    MaxPooling2D(pool_size=(3, 3), strides=(2, 2)),
    Flatten(),
    Dense(4096, activation='relu'),
    Dropout(0.5),
    Dense(4096, activation='relu'),
    Dropout(0.5),
    Dense(1000, activation='softmax')
])
model.compile(optimizer=Adam(), loss='categorical_crossentropy', metrics=['accuracy'])
model.summary()

实验结果与讨论#

作者通过实验验证了提出方法的有效性，具体步骤如下：

数据集: 使用来自中国北方油田的实际数据进行实验。
分类准确率: AlexNet-SVM方法的总体分类准确率超过99%，显著优于传统方法。

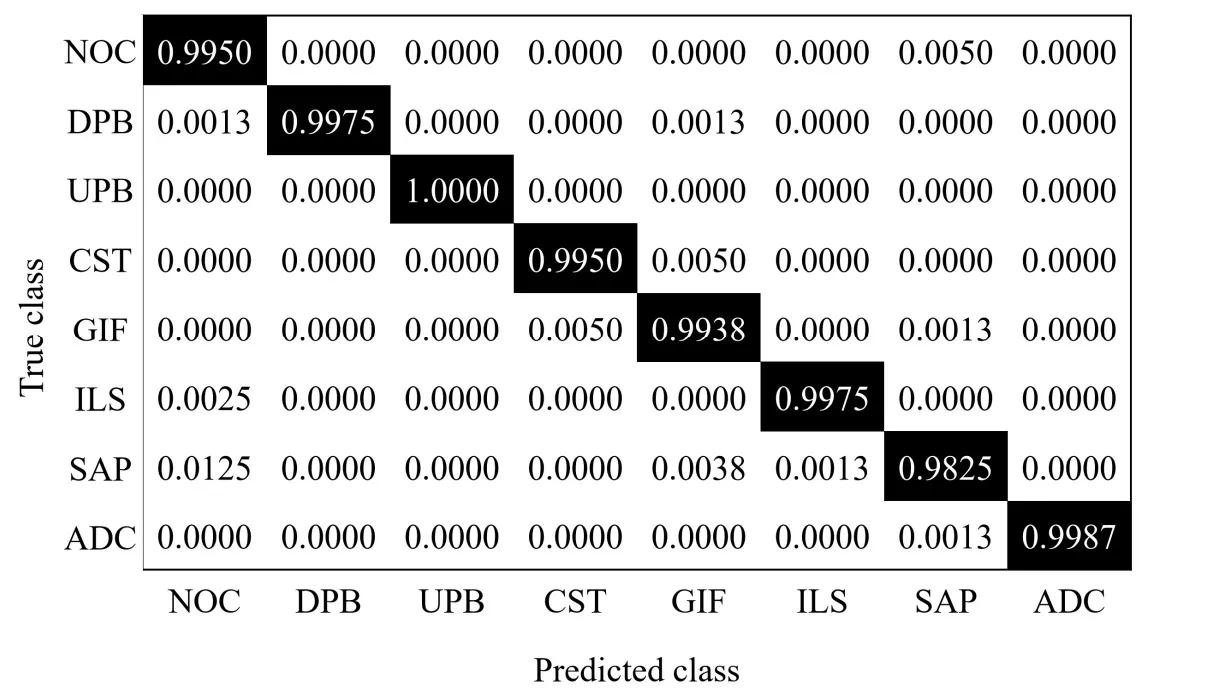
结论#

本文提出的基于AlexNet和SVM的方法有效地自动识别抽油杆泵系统的工作状态，减少了人工干预，提高了识别准确率。未来的研究将收集更多数据，进一步改进算法性能，以应对更复杂的工业应用场景。

2.论文题目：使用机器学习诊断抽油杆泵井的操作条件和传感器故障#

Local image

摘要#

在抽油杆泵井中，由于缺乏对操作条件或传感器故障的早期诊断，许多问题可能会被忽视，从而增加停机时间和生产损失。本文采用机器学习算法，对来自38口井的超过50000张示功图进行了诊断测试，评估了决策树、随机森林和XGBoost三种算法的性能，并使用了傅里叶、Wavelet和负载值三种描述符。结果表明，该方法在75%的测试中准确率超过92%，最高达99.84%。

关键词#

抽油杆泵，机器学习算法，示功图，石油工业

方法论详细介绍#

数据集#

本研究使用来自巴西Mossoró地区38口抽油杆泵井的超过50000张示功图。这些图由专家分类，分为八种操作模式和两种常见的传感器故障。研究中进行了60次测试，数据集的分布如表1所示。

表1. 数据集分布#

操作模式或故障类型	样本数量
正常	10282
气体干扰	260
液柱	38298
活塞阀泄漏	67
站立阀泄漏	172
杆断裂	29
气锁	6
管柱锚故障	30
传感器故障 - 旋转卡片	895
传感器故障 - 线卡片	73

特征提取#

傅里叶描述符：利用傅里叶变换对示功图进行特征提取。傅里叶描述符可以通过离散傅里叶变换（DFT）计算轮廓的傅里叶系数。公式如下： $a(k) = \frac{1}{N} \sum_{k=0}^{N-1} z(k)e^{-j2\pi nk/N}$ 其中， $z(k)$ 是复数表示的轮廓点， $N$ 是轮廓点的数量。
小波描述符：使用连续小波变换（CWT）进行特征提取。小波变换基于小波函数的多分辨率分析。公式如下： $Cw(s, b) = \frac{1}{\sqrt{|s|}} \int z(k) \psi \left( \frac{k-b}{s} \right) dk$ 其中， $\psi$ 是小波函数， $s$ 是尺度因子， $b$ 是平移因子。
负载值：利用示功图中的负载值作为特征。通过归一化处理，将不同井的示功图负载值统一到相同的尺度。

机器学习算法#

决策树（Decision Tree）：基于训练样本构建决策模型，通过决策节点和叶子节点对数据进行分类。
随机森林（Random Forest）：集成算法，使用多个决策树的投票结果进行分类。每棵树仅使用部分训练数据，最终结果为多数投票结果。
XGBoost：增量树模型，基于梯度提升算法。通过不断调整权重，提高分类准确率。
平衡数据集和超参数调整：由于数据集不平衡，采用随机过采样技术平衡数据集。此外，使用网格搜索和随机搜索进行超参数调整，选择最佳参数组合提高模型性能。

结果分析#

在测试中，模型的准确率在75%的测试中超过92%，最高达99.84%。以下是一个决策树模型的代码示例：

from sklearn.tree import DecisionTreeClassifierfrom sklearn.model_selection import train_test_splitfrom sklearn.metrics import accuracy_score
# 假设 data 为示功图特征，labels 为对应标签
X_train, X_test, y_train, y_test = train_test_split(data, labels, test_size=0.2, random_state=42)
# 创建决策树模型
clf = DecisionTreeClassifier()
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)print(f'模型准确率: {accuracy}')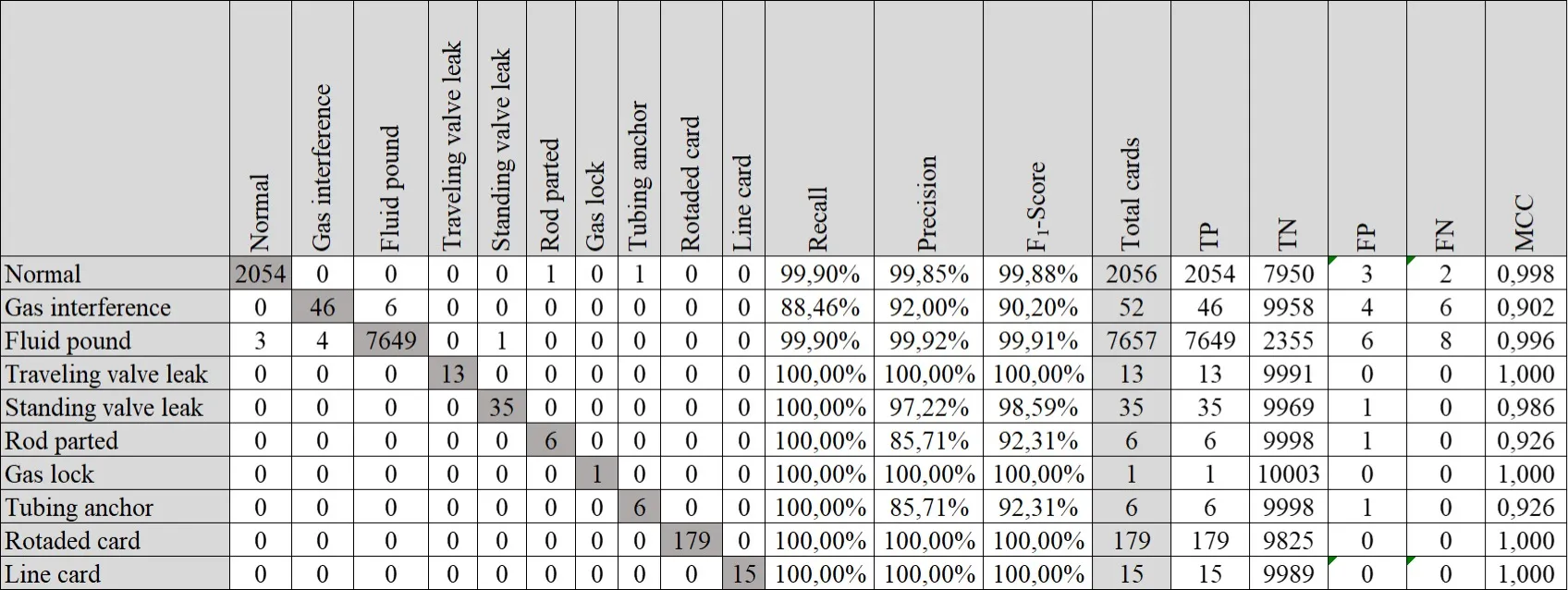

Local image

结论#

本文提出的基于机器学习的诊断方法能够有效识别抽油杆泵井的操作条件和传感器故障，具有高准确率和较强的鲁棒性。未来研究可以进一步优化算法，提高模型在不同场景下的适用性。

3.论文题目：抽油杆泵系统的模型预测自动控制及仿真案例研究#

Local image

摘要#

本研究通过自动控制井中的流体高度和井底压力来加速油气资源的回收。尽管文献中有很多研究展示了通过确定目标井底压力来显著增加回收油量，但很少考虑如何控制该值。本研究通过维护井底压力或流体高度来实现这些益处。采用移动视界估计（MHE）仅使用常见的地面测量数据确定不确定的井参数。模型预测控制器（MPC）调整抽油杆泵的冲程速度以维持流体高度。使用带互补性约束的数学程序和非线性规划求解器在接近实时的情况下找到解决方案。结合了抽油杆、井和储层模型来模拟动态井况，并通过大规模求解器进行同时优化。MPC通过保持最佳流体高度来增加累计石油产量，相比传统的停泵控制方法，效果更显著。

关键词#

抽油杆泵，模型预测控制，优化，储层建模

方法论详细介绍#

概述#

本研究提出了一种新颖的自动控制系统，结合了抽油杆泵、井和储层模型，通过维持最佳流体高度来最大化石油产量，并减少设备损坏。具体方法包括移动视界估计（MHE）和模型预测控制（MPC）。

井和抽油杆系统#

井和抽油杆建模#

模型包括井底组件和表面驱动单元的运动学方程。流体通过井套管的穿孔进入井筒并在生产油管和井套管之间的环形空间积累。通过一个四杆机构驱动抽油杆带动井底正排量泵提升流体到地面。

运动学方程#

表面单元的运动学方程描述了抽油杆泵的垂直位置，公式如下：

u(0, \theta(t)) = L_3 \left[ \arcsin\left( \frac{L_1 \sin \theta(t)}{h} \right) + \arccos\left( \frac{h^2 + L_2^3 - L_4^2}{2L_3h} \right) \right]

其中 $h = \sqrt{L_1^2 + L_2^2 + 2L_1L2 \cos(\theta(t))}$ 。

动力学方程#

结合摩擦力和负载力矩，动力学方程为：

J_0 \frac{d\omega}{dt} = -B\omega + T_{net}

其中 $T_{net}$ 为净力矩， $J_0$ 为惯性矩， $B$ 为摩擦系数。

波动方程#

波动方程用于模拟抽油杆的动力学，公式为：

\frac{\partial^2 u(x, t)}{\partial t^2} = a^2 \frac{\partial^2 u(x, t)}{\partial x^2} - \pi a \nu \frac{2L}{\partial u(x, t)}{\partial t} - \left(1 - \frac{\rho_w \gamma}{\rho_r} \right) g

边界条件为：

u(0, t) = F(t), \quad P_{bd}(t) = \alpha p + \beta \frac{\partial u(x_f, t)}{\partial x}

其中， $F(t)$ 为地面负载， $P_{bd}(t)$ 为泵边界条件。

储层建模#

储层模型假设流体为不可压缩液体，公式为：

q_{in} = \frac{kh(P - P_{wf})}{141.2B_0\mu \left( \frac{1}{2} \ln \left( \frac{4A}{\gamma C_A r_w^2} \right) + S \right)}

并结合材料平衡方程，公式为：

\frac{dm}{dt} = \rho_w \gamma (q_{in} - q_{prod})

其中 $q_{in}$ 为储层流入速率， $q_{prod}$ 为生产流体速率。

经济学考量#

经济可行性通过净现值（NPV）衡量，公式为：

NPV = \int S(t) e^{-rt} dt - C_{initial}

其中 $S(t)$ 为利润率，定义为收入率和支出率之差。

移动视界估计（MHE）和模型预测控制（MPC）#

MHE： MHE利用历史数据拟合模型参数以进行实时估计。目标函数为最小化测量数据和模型预测值之间的平方误差： $\min_{x, y, p} \Phi = (y_x - y)^T W_m (y_x - y)$
MPC： MPC通过调整可操作变量来最小化受控变量轨迹和模型预测之间的误差。目标函数为： $\min_{x, y, u} \Phi = W_{hi}^T e_{hi} + W_{lo}^T e_{lo} + y^T c_y + \Delta u^T c_{\Delta u}$

代码示例#

下面是一个使用Python实现MPC控制器的示例代码：

m = GEKKO(remote=False)
# 定义变量
SPM = m.Var(value=10)
Tnet = m.Var(value=10)
fluid_height = m.Var(value=100)
# 定义参数
qin = m.Param(value=5)
qprod = m.Param(value=5)
# 定义方程
m.Equation(fluid_height.dt() == (qin - qprod) / (Accasing - Actubing))
m.Equation(Tnet == 10 * SPM)
# 目标函数
m.Obj(fluid_height - 100)
# 求解
m.options.IMODE = 6
m.solve()
print(f'Optimal SPM: {SPM.value[0]}')

结论#

本文提出的基于MHE和MPC的方法通过优化抽油杆泵的冲程速度，有效地控制井底压力和流体高度，最大化石油产量，并减少设备损坏。在未来的研究中，可以进一步优化该模型以适应更复杂的井况和储层动态。

4.论文题目：Diagnosis for Sucker Rod Pumps Using Bayesian Networks and Dynamometer Card#

Local image

摘要#

作者们提出了一种基于贝叶斯网络和游标图的计算机辅助诊断方法，以确保油田的利益和提高石油采收率。游标图作为重要的信息资源，广泛用于油田工程的监控和诊断。论文的核心方法是将游标图的坐标转换，以便进行负载分析，并从中提取五个统计特征和香农熵，作为贝叶斯网络的输入。实验结果表明，该方法在诊断抽油杆泵工作状态方面是有效的。

方法论详细介绍#

一、游标图特征提取#

统计特征#

论文从游标图中提取了五个统计特征：

最大负载和最小负载之比 $\eta$
均方根 (RMS)
偏度 (Skewness)
峰度 (Kurtosis)
形状因子 (Shape Factor)

数学公式#

最大负载和最小负载之比： $\eta = \frac{\max(x) - \min(x)}{\max(x)}$
均方根 (RMS)： $\text{RMS} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (x_i - \mu)^2}$
偏度 (Skewness)： $\text{Skewness} = \frac{1}{n} \sum_{i=1}^{n} \left(\frac{x_i - \mu}{\sigma}\right)^3$
峰度 (Kurtosis)： $\text{Kurtosis} = \frac{1}{n} \sum_{i=1}^{n} \left(\frac{x_i - \mu}{\sigma}\right)^4$
形状因子 (Shape Factor)： $\text{Shape Factor} = \frac{\sum_{i=1}^{n} x_i}{\sum_{i=1}^{n} |x_i|}$

香农熵#

香农熵用于度量信号的不确定性和随机性： $EDC = - \sum_{t=1}^{T} x(t) \log x(t)$

二、动态贝叶斯网络诊断模型#

贝叶斯网络 (BN) 是一种概率图模型，用于表示随机变量之间的因果关系。论文使用了一种特殊类型的BN，称为条件高斯网络 (Conditional Gaussian Network, CGN)，用于实现连续变量的概率推断。CGN包含两种节点：离散节点和高斯节点。

贝叶斯网络的联合概率分布可表示为： $P(X_1, X_2, \ldots, X_n) = \prod_{i=1}^{n} P(X_i | \text{Pa}(X_i))$ 其中， $\text{Pa}(X_i)$ 是节点 $X_i$ 的父节点集合。

CGN中，高斯节点的条件分布可以表示为： $P(Y | X = x_k) \sim \mathcal{N}(\mu_k, \sigma_k)$

模型的训练过程包括以下步骤：

配置结构基于过程动态。
设置先验概率分布。
逐个输入样本进行训练，更新信念直到获得最终模型。

对于新样本 $O_{T+1}$ ，使用训练好的模型进行分类： $S = \arg \max_{s \in S} P(O_{T+1} | S = s)$

代码示例#

以下是一个简单的Python代码示例，用于计算特征并训练贝叶斯网络：

import numpy as npfrom sklearn.preprocessing import StandardScalerfrom pomegranate import BayesianNetwork, ConditionalGaussianDistribution
# 示例数据
data = np.array([[1.5, 2.0, 3.5], [2.5, 3.0, 4.0], [3.5, 4.0, 5.5]])
# 特征提取def extract_features(data):
    max_load = np.max(data, axis=1)
    min_load = np.min(data, axis=1)
    rms = np.sqrt(np.mean(data**2, axis=1))
    skewness = np.mean((data - np.mean(data, axis=1, keepdims=True))**3, axis=1) / np.std(data, axis=1)**3
    kurtosis = np.mean((data - np.mean(data, axis=1, keepdims=True))**4, axis=1) / np.std(data, axis=1)**4
    shape_factor = np.mean(data, axis=1) / np.mean(np.abs(data), axis=1)
    return np.column_stack((max_load - min_load, rms, skewness, kurtosis, shape_factor))

features = extract_features(data)
# 数据标准化
scaler = StandardScaler()
features = scaler.fit_transform(features)
# 贝叶斯网络训练
model = BayesianNetwork.from_samples(features, algorithm='exact')
# 新样本分类
new_sample = np.array([[2.0, 3.0, 4.5]])
new_features = scaler.transform(extract_features(new_sample))
result = model.predict(new_features)print(result)

结论#

这篇论文提出了一种基于贝叶斯网络和游标图的抽油杆泵工作状态诊断方法。通过转换游标图坐标并提取统计特征和香农熵，该方法能够有效地诊断抽油杆泵的正常和故障状态。实验结果验证了该方法的有效性和实用性。

5.论文题目：Application of CNN-LSTM in Gradual Changing Fault Diagnosis of Rod Pumping System#

Local image

摘要#

提出了一种结合卷积神经网络（CNN）和长短期记忆网络（LSTM）的新方法，用于诊断抽油杆泵系统中的渐变故障。渐变故障是一种特殊的故障类型，其特征在初期并不明显，只有在对井造成不可逆损害后才能识别。该方法利用CNN提取指示图的多层抽象特征，并通过LSTM识别时间序列的变化。相比传统的数学模型诊断方法，CNN-LSTM克服了传统方法的不明确假设条件，提高了诊断的准确性。

方法论详细介绍#

一、渐变故障的定义与特征参数#

渐变故障定义#

渐变故障包括环空损失、套管腐蚀、出砂、结垢和泵筒磨损等。传统方法基于经验判断，准确性低且容易误判。论文提出使用主成分分析（PCA）来更准确地识别渐变故障，通过计算指示图相似性因子（SPCA）来区分故障类型：

S_{PCA} = \frac{\text{trace}(R^T T^T T R)}{\sum_{i=1}^{k} \lambda_{l_i} \lambda_{m_i}}

其中， $R$ 和 $T$ 分别为PCA模型的子空间， $\lambda_{l_i}$ 和 $\lambda_{m_i}$ 为特征值。

特征参数#

多视图连续指示图的融合可以有效保留有用信息，从而识别渐变故障。图2显示了结垢过程中悬点载荷的变化，载荷在故障发生时急剧增加。上冲程和下冲程的载荷变化反映了结垢的发生。

二、CNN-LSTM模型#

CNN结构#

CNN包含输入层、卷积和池化层以及全连接层。输入层接收多幅指示图序列，通过卷积和池化层提取特征。卷积层使用过滤器 $W_c$ 来提取特征向量：

C = \text{ReLU}(X \ast W_c + b)

池化层使用最大池化操作：

X_{\text{map}} = [\max(C)]

LSTM结构#

LSTM增加了输入门、输出门和遗忘门，解决了RNN中的梯度消失问题。LSTM节点的传输方程如下：

c_n, h_n = \tanh(W_c \cdot X_j + b)

其中， $X_j$ 为输入向量， $W_c$ 为权重矩阵， $b$ 为偏置向量。

三、框架概述#

论文提出的CNN-LSTM框架包括三个主要组件：指示图分类、CNN-LSTM训练和系统应用。

指示图分类#

从数据集中准备多幅连续指示图，作为完整周期的数据输入。

CNN-LSTM训练#

使用CNN提取指示图特征，并将这些特征输入LSTM以获得特征序列。然后，使用softmax分类器对LSTM输出进行分类。

系统应用#

使用训练好的CNN-LSTM模型进行渐变故障识别，并将识别结果分类为对应的故障类型。

代码示例#

以下是一个使用Python实现CNN-LSTM模型的代码示例：

import numpy as npfrom tensorflow.keras.models import Sequentialfrom tensorflow.keras.layers import Conv2D, MaxPooling2D, Flatten, LSTM, Dense, TimeDistributed
# 构建CNN模型
cnn = Sequential()
cnn.add(Conv2D(32, (3, 3), activation='relu', input_shape=(64, 64, 1)))
cnn.add(MaxPooling2D(pool_size=(2, 2)))
cnn.add(Conv2D(64, (3, 3), activation='relu'))
cnn.add(MaxPooling2D(pool_size=(2, 2)))
cnn.add(Flatten())
# 构建LSTM模型
model = Sequential()
model.add(TimeDistributed(cnn, input_shape=(10, 64, 64, 1)))
model.add(LSTM(50, activation='relu'))
model.add(Dense(1, activation='sigmoid'))
# 编译模型
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
# 假设X_train和y_train是训练数据# X_train形状为(样本数, 时间步长, 高度, 宽度, 通道数)# y_train形状为(样本数,)
model.fit(X_train, y_train, epochs=10, batch_size=32)

结论#

这篇论文提出了一种结合CNN和LSTM的方法，用于诊断抽油杆泵系统中的渐变故障。利用CNN的层次结构提取指示图特征，并通过LSTM识别时间序列的变化，实验结果表明该方法的准确率达到了98.4%。与传统方法相比，CNN-LSTM方法在处理大数据集和提高数据利用率方面显示了绝对优势。 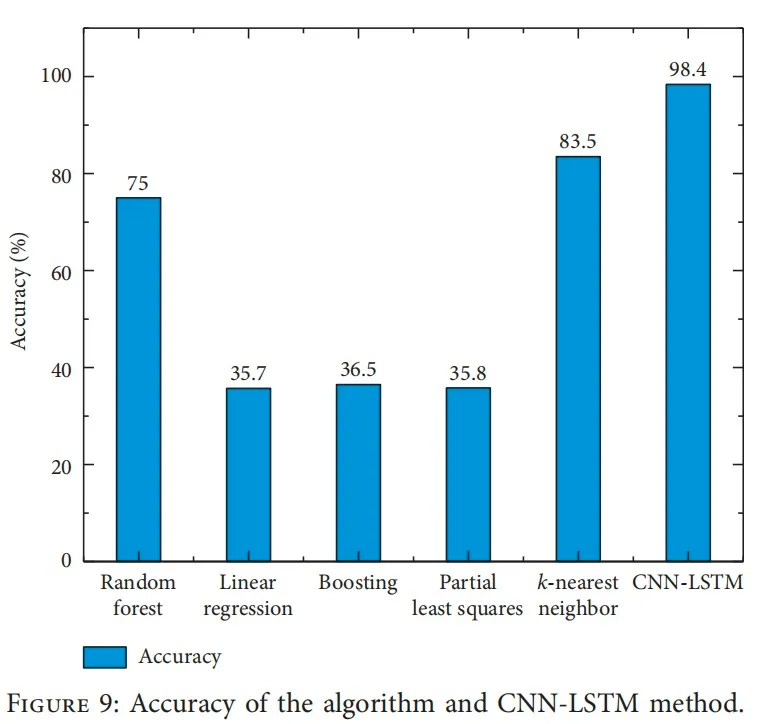Local image

6.论文题目：Predicting Failures and Optimizing Performance in Rod Pumps using Data Science Models#

Local image

摘要#

由Mike Pennell在第13届Sucker Rod Pumping Workshop上发表，主要讨论如何利用数据科学模型预测抽油杆泵的故障并优化其性能。论文介绍了机器学习（ML）在抽油杆泵中的应用，阐述了关键的ML术语和概念，展示了各种模型的工作原理和性能，特别是随机森林和梯度提升树等集成模型，并讨论了这些模型在实际应用中的结果和效益。

方法论详细介绍#

特征提取和归一化#

特征提取#

论文中提到对抽油杆泵进行多维度监控，包括套管压力、油管压力、泵填充率、运行百分比、峰值负载、最小负载和液体负载等。这些信号被用作特征，以便数学模型能够进行处理和分析。

归一化#

信号归一化是将信号与正常信号进行比较，使得不同井的信号在数学模型中具有可比性。归一化方法包括：

原始信号
归一化值
归一化方差

归一化后的值范围从-5到5，0表示正常；归一化方差范围从0到10，小于1表示正常。

机器学习模型#

模型类型#

论文主要使用决策树模型，包括随机森林（Random Forest, RF）和梯度提升树（Gradient Boosted Trees, GBT）。这些集成模型由数十到数百棵树组成，每棵树进行投票。

性能测量#

准确率 (Accuracy): $(TP + TN) / (TP + FP + TN + FN)$
精确率 (Precision): $TP / (TP + FP)$
召回率 (Recall/Sensitivity): $TP / (TP + FN)$

模型训练和验证#

训练集用于训练模型，测试集用于评估模型性能。交叉验证用于评估模型在未见过的数据上的表现。

三、神经网络模型#

神经网络#

论文中提到神经网络主要用于分类游标图形状，但不足以进行预测。

集成模型#

集成模型的工作机制包括以下几个层次：

特征提取层: 计算用于高层模型的所需特征。
基础周期诊断: 基于相似特征/模式识别高风险周期。
事件诊断: 收集完整事件信息，评估可能性。
事件分类: 解决基础模型之间的冲突，做出最终预测。

代码示例#

以下是一个简单的Python代码示例，演示如何使用随机森林模型进行抽油杆泵故障预测：

import numpy as np
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, precision_score, recall_score

# 示例数据
X = np.random.rand(1000, 24)  # 24个特征
y = np.random.randint(2, size=1000)  # 二分类标签

# 分割数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 训练随机森林模型
rf = RandomForestClassifier(n_estimators=100, max_depth=19, random_state=42)
rf.fit(X_train, y_train)

# 预测
y_pred = rf.predict(X_test)

# 计算性能指标
accuracy = accuracy_score(y_test, y_pred)
precision = precision_score(y_test, y_pred)
recall = recall_score(y_test, y_pred)

print(f'Accuracy: {accuracy:.2f}')
print(f'Precision: {precision:.2f}')
print(f'Recall: {recall:.2f}')

结论#

这篇论文展示了如何利用数据科学模型（尤其是随机森林和梯度提升树）来预测抽油杆泵的故障并优化其性能。通过归一化处理和特征提取，使得不同井的信号在模型中具有可比性。模型的性能测量包括准确率、精确率和召回率。集成模型在处理复杂数据和提高故障预测准确性方面显示了显著优势。