一、从 MLP 讲起#

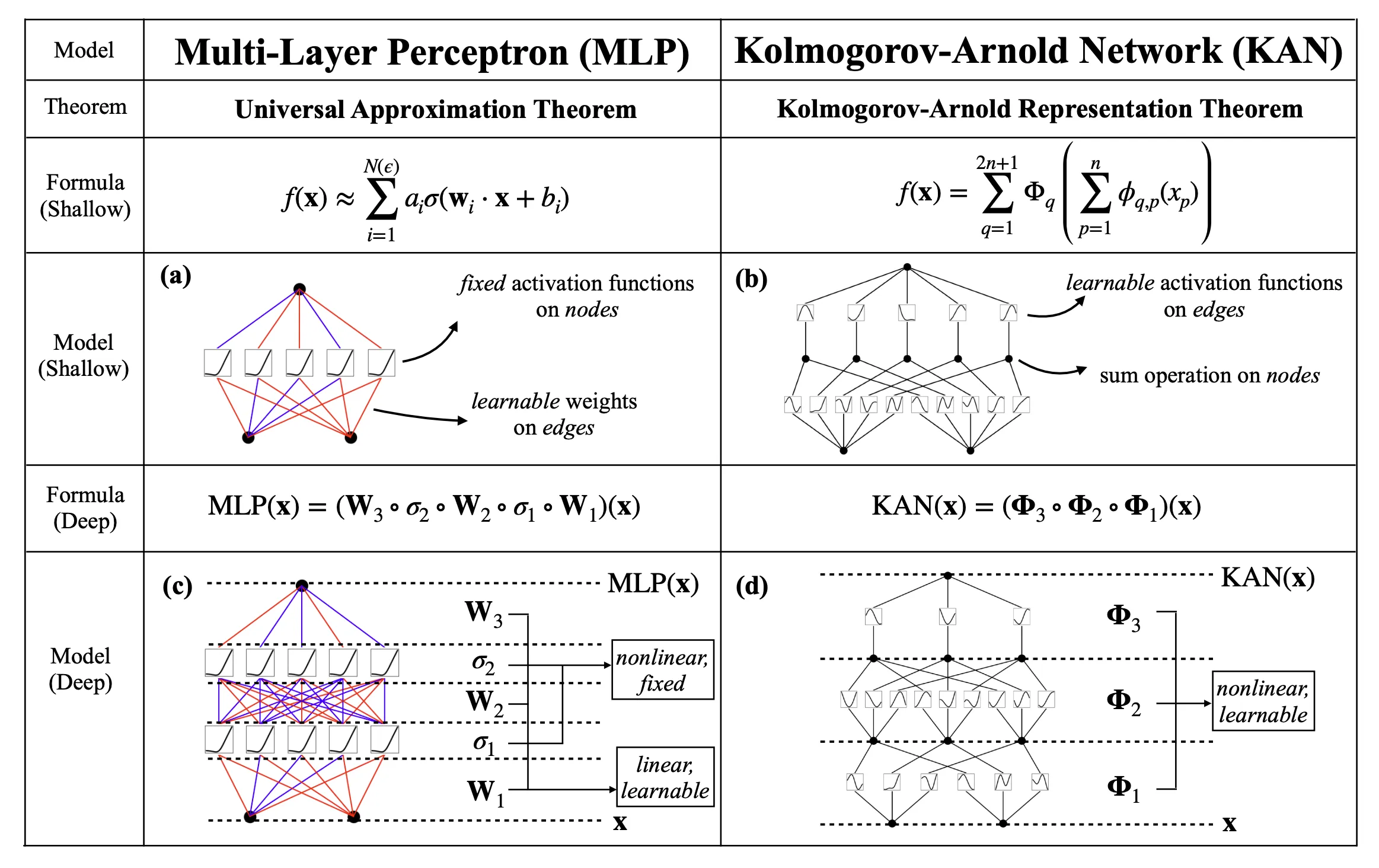
多层感知机（MLP，Multi-Layer Perceptron）#

多层感知机（MLP，Multi-Layer Perceptron）是一种全连接的前馈神经网络，通常用于解决分类和回归问题。MLP 由多层组成，每一层都包括多个节点或神经元。这些神经元通常具有非线性激活函数，如 ReLU 或 Sigmoid，以帮助网络学习和近似复杂的非线性函数。MLP 的结构通常包括一个输入层，若干隐藏层，以及一个输出层。

MLP（多层感知机）的基本原理和结构#

原理#

MLP 是一种基础的神经网络架构，主要通过层与层之间的全连接实现输入到输出的映射。MLP 的核心在于其能够通过足够的隐藏层和神经元数量逼近任何连续函数，这一能力基于通用逼近定理。这个定理指出，只要有足够的神经元和适当的激活函数，MLP 可以以任意精度逼近任何非线性连续函数。

结构#

• 节点/神经元连接：在 MLP 中，每个神经元都与前一层的所有神经元连接，并向下一层的每个神经元传递信息。
• 激活函数：MLP 中的每个节点都使用非线性激活函数处理其输入，常见的激活函数包括 ReLU、Sigmoid 和 Tanh。这些固定且非线性的激活函数帮助网络捕捉复杂的数据关系。

二、MLP导致了深度学习大厦的脆弱#

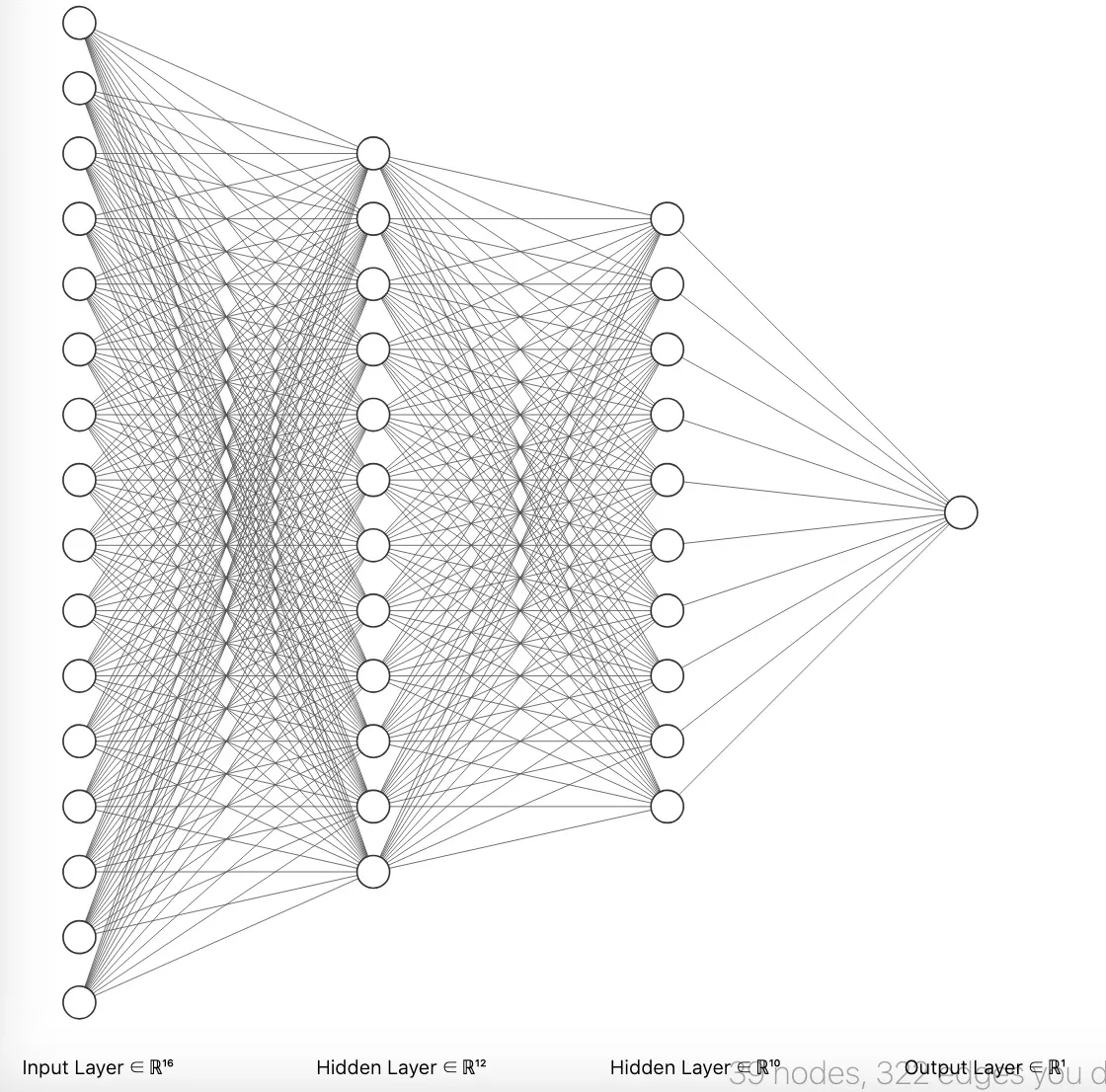多层感知机（MLP）在深度学习的发展中确实起到了重要的基础作用，但它也展示出了一些结构上的脆弱性，特别是在面对复杂的现实世界应用时。因为它的全连接网络。下面是它的一些缺点。

梯度消失和爆炸（Vanishing and Exploding Gradients）#

在训练 MLP 时，尤其是网络层数较深的时候，通过反向传播算法更新权重时可能会遇到梯度消失或爆炸的问题。梯度消失是指梯度在传递过程中逐渐变小，最终导致深层网络中的权重几乎不更新；梯度爆炸则是梯度急剧增大，使得权重更新过度，导致网络不稳定。这两种现象都会严重影响学习过程和网络的性能。

参数效率低#

MLP 通常使用全连接层，这意味着每层的每个神经元都与前一层的所有神经元相连接，导致参数数量迅速增加，尤其是对于输入维度很高的数据。这不仅增加了计算负担，也增加了模型过拟合的风险。

可解释性差#

MLP 的决策过程通常是不透明的，这使得理解和解释模型的行为变得困难。在需要高度可信赖的应用中，如医疗诊断和金融服务，模型的不可解释性可能会成为一个严重的障碍。

长期依赖问题#

虽然 MLP 理论上可以逼近任何函数，但在实际应用中，它们很难捕捉到输入序列中的长期依赖关系（长时间跨度的相关信息）。这一点在处理时间序列或自然语言处理任务时尤为明显，而循环神经网络（RNN）和 Transformer 在这些任务中通常表现得更好。

尽管存在这些问题，MLP 仍然是深度学习和机器学习中一个重要的模型，对于一些问题，它能够提供足够好的解决方案。然而，为了克服上述限制，研究者们开发了更加高级的神经网络架构，如卷积神经网络（CNNs）、循环神经网络（RNNs）和注意力机制（Attention Mechanisms），这些技术能够更好地处理具有空间或时间结构的数据，并提高模型的泛化能力和解释性。

三、KAN 网络和 MLP 网络对比#

1. 网络结构#

MLP:

• 节点上的固定激活函数: MLP 中的每个节点（神经元）都使用固定的激活函数（如 ReLU、Sigmoid）。
• 线性权重矩阵: 每层之间的连接使用线性权重矩阵。
• 求和操作: 节点上进行加权求和并应用激活函数。

KAN:

• 边上的可学习激活函数: KAN 中的激活函数不是固定在节点上，而是固定在边上，即每个权重是一个可学习的单变量函数（如样条函数）。
• 无线性权重矩阵: KAN 没有传统的线性权重矩阵，所有权重都是非线性的单变量函数。
• 简单求和: 节点上只进行简单求和，不应用任何非线性操作。

2. 数学表达#

MLP:

• 表示为线性变换和非线性激活函数的交替应用： $$MLP(x) = (W_{L-1} \circ \sigma \circ W_{L-2} \circ \sigma \circ \cdots \circ W_0)(x)$$

KAN:

• 表示为单变量函数的矩阵的组合： $$KAN(x) = (\Phi_{L-1} \circ \Phi_{L-2} \circ \cdots \circ \Phi_0)(x)$$
• 其中每个 $\Phi_l$ 是一个包含可学习单变量函数的矩阵。

3. 可解释性#

MLP:

• 解释性差: MLP 的非线性变换固定在节点上，难以直接解释每个权重的具体意义。
• 需要后处理工具: 解释 MLP 模型通常需要复杂的后处理工具和技术。

KAN:

• 高可解释性: 由于激活函数是可学习的单变量函数，且这些函数可以直接可视化，因此 KAN 模型更容易解释。
• 用户互动: 用户可以直接与 KAN 模型互动，通过设置或修改激活函数的形式来理解模型。

4. 精度和效率#

MLP:

• 较低的参数效率: 为了达到高精度，MLP 通常需要较多的参数和更深的网络结构。
• 扩展性有限: MLP 在处理高维数据时，受“维数灾难”影响较大，扩展性较差。

KAN:

• 高参数效率: KAN 通过使用可学习的激活函数，通常可以在较少的参数下达到或超过 MLP 的精度。
• 更好的扩展性: KAN 能更好地处理高维数据，尤其是具有组合结构的数据，能够更有效地克服“维数灾难”。

5. 应用场景#

MLP:

• 广泛应用: MLP 是深度学习中的基础模型，广泛应用于分类、回归和生成模型等各种任务中。
• 需要优化: 在复杂任务中，MLP 的表现需要大量的调参和优化工作。

KAN:

• 科学发现: 由于其高精度和高可解释性，KAN 特别适用于科学研究和发现，如数学和物理规律的重新发现。
• 数据拟合和 PDE 求解: KAN 在数据拟合和偏微分方程求解方面表现出色，能够以更少的参数达到更高的精度。

四、KAN 的架构细节#

详细架构#

基本结构#

1. KANs 中的每个权重参数被替换为可学习的单变量函数，这些函数被参数化为样条函数。
2. KANs 的节点仅对传入信号进行求和，不应用任何非线性变换。
3. KANs 不包含线性权重矩阵，所有权重参数都是可学习的 1D 函数。

数学表示#

1. 根据 Kolmogorov-Arnold 定理，任何平滑函数 ( f(x) ) 可以表示为一系列单变量函数和求和操作的组合： $$f(x) = \sum_{q=1}^{2n+1} \Phi_q \left( \sum_{p=1}^n \varphi_{q,p}(x_p) \right)$$
2. KAN 的每一层由一个 1D 函数矩阵组成： $$\Phi = \{ \varphi_{q,p} \}, \quad p = 1, 2, \cdots, n_{in}, \quad q = 1, 2 \cdots, n_{out}$$

计算过程#

1. KAN 的计算图由多层组成，每层的输入和输出通过可学习的 1D 函数相连。
2. 层与层之间的激活函数表示为： $$x_{l+1,j} = \sum_{i=1}^{n_l} \varphi_{l,j,i}(x_{l,i})$$
3. 通过这样的层次结构，KAN 的输出可以表示为： $$KAN(x) = (\Phi_{L-1} \circ \Phi_{L-2} \circ \cdots \circ \Phi_0)(x)$$

优化技巧#

1. 残差激活函数: 在激活函数中包含一个基函数 ( b(x) )，使得激活函数成为基函数和样条函数的和： $$\varphi(x) = w (b(x) + \text{spline}(x))$$ 其中，基函数 ( b(x) ) 通常为 ( \text{silu}(x) = x/(1 + e^{-x}) )，样条函数则由 B 样条基函数的线性组合表示。
2. 初始化: 激活函数初始化为接近零的样条函数，权重 ( w ) 根据 Xavier 初始化方法进行初始化。
3. 样条网格更新: 在训练过程中动态更新每个样条网格，以确保激活值在有界区域内变化。

参数数量#

1. 对于深度为 ( L ) 且每层宽度为 ( N ) 的 KAN，假设每个样条函数的阶数为 ( k )，网格点数为 ( G )，则总参数数量为： $$O(N^2L(G+k))$$

解释性和简化技术#

1. 稀疏化: 通过 ( L1 ) 正则化和熵正则化对 KAN 进行稀疏化。
2. 可视化: 激活函数的透明度与其平均幅值成比例，较小的激活函数被淡化以突出重要的函数。
3. 剪枝: 对于不重要的节点进行剪枝，保留重要节点的输入和输出得分高于某一阈值。
4. 符号化: 提供接口将激活函数设置为指定的符号形式，并通过迭代网格搜索和线性回归拟合仿射参数。

五、实验论证#

实验目标#

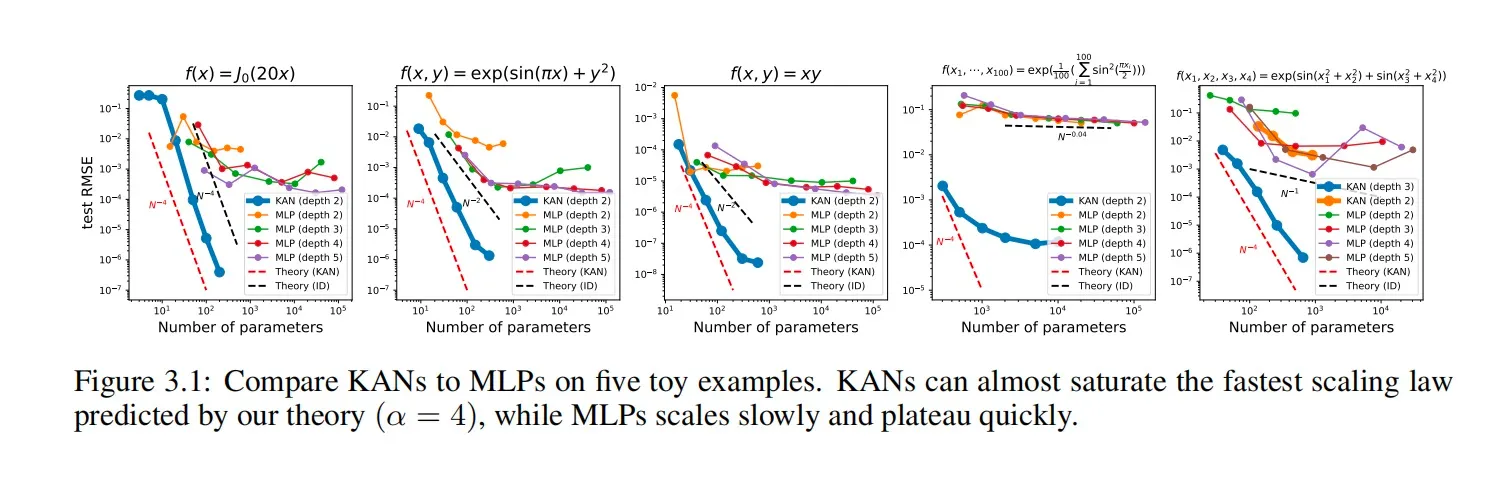实验主要通过与 MLP（多层感知器）进行比较，验证 KAN（Kolmogorov-Arnold Networks）在各种任务中的性能优势，包括数据拟合、偏微分方程（PDE）求解等。

1. 数据拟合与 PDE 求解#

实验设置：

• 构建五个已知具有光滑 Kolmogorov-Arnold 表示的示例函数。
• 比较不同深度和宽度的 MLP 与 KAN 在这些函数上的拟合效果。

示例函数：

1. ( f(x) = J_0(20x) )（Bessel 函数）
2. ( f(x, y) = \exp(\sin(\pi x) + y^2) )
3. ( f(x, y) = xy )
4. 高维函数 ( f(x_1, \cdots, x_{100}) = \exp \left( \frac{1}{100} \sum_{i=1}^{100} \sin^2(\pi x_i / 2) \right) )
5. 四维函数 ( f(x_1, x_2, x_3, x_4) = \exp \left( \frac{1}{2} (\sin(\pi (x_1^2 + x_2^2)) + \sin(\pi (x_3^2 + x_4^2))) \right) )

训练方法：

• KAN 通过增加样条网格的数量进行训练，从较少的参数开始，然后逐步增加网格点数。
• MLP 则通过调整深度和宽度进行训练。

结果：

• 在所有示例函数上，KAN 的拟合误差（RMSE）随参数数量增加的缩放率均优于 MLP。
• KAN 能够以较少的参数数量达到或超过 MLP 的精度，尤其是在高维数据上表现更为明显。

2. 特殊函数拟合#

实验设置：

• 选择了 15 个常见于数学和物理的特殊函数。
• 比较不同深度和宽度的 MLP 与 KAN 在这些函数上的拟合效果。

特殊函数示例：

• Jacobian 椭圆函数
• 不完全椭圆积分
• 第一类和第二类的 Bessel 函数
• 关联 Legendre 函数
• 球谐函数

结果：

• KAN 在所有特殊函数上的拟合误差（RMSE）均低于 MLP。
• KAN 的 Pareto 前沿（参数数量和 RMSE 的关系曲线）优于 MLP，即在相同参数数量下，KAN 的误差更小。

3. 费曼方程数据集#

实验设置：

• 使用费曼方程数据集，包含一系列物理公式。
• 比较人工构建的 KAN 和通过剪枝技术自动发现的 KAN 在这些数据集上的表现。

结果：

• 人工构建的 KAN 和自动发现的 KAN 都表现出色，后者在某些情况下甚至优于前者。
• KAN 在费曼方程数据集上的表现优于 MLP，尤其是在参数效率和精度上。

4. 连续学习#

实验设置：

• 评估 KAN 在连续学习任务中的表现，即模型在训练新任务时是否会遗忘之前学到的知识（灾难性遗忘）。

结果：

• KAN 在连续学习任务中表现良好，没有明显的灾难性遗忘现象。
• 通过动态调整样条网格，KAN 能够有效适应新的任务，并保持之前任务的性能。

实验总结#

1. 精度优势： KAN 在多种任务和数据集上均表现出优于 MLP 的拟合精度，尤其在高维数据和复杂函数拟合方面。
2. 参数效率： KAN 通过使用可学习的激活函数（样条函数），在较少的参数下达到了更高的精度，提高了模型的参数效率。
3. 可解释性： KAN 的可解释性较强，激活函数的可视化和符号化使得模型更易于理解和调试。
4. 灵活性： KAN 可以通过增加样条网格点数动态调整模型复杂度，适应不同的任务需求，显示出较高的灵活性。