939 words
5 minutes
MIT概率论笔记第5节课离散随机变量
欢迎来到离散随机变量这一章节
2.1 基本概念
离散随机变量是指取值为分隔的、可数的数值集的随机变量。换句话说,这种变量的可能结果是可列举的,例如整数序列。这与连续随机变量不同,后者可以在某个区间内取任意值。在深度学习中,离散随机变量常用于描述分类任务的输出,如图像识别中的标签预测,每个标签可以视为一个离散值。在离散随机变量的研究中,我们通常关注变量取整数值的概率分布。理解离散随机变量的行为,可以帮助我们在设计和训练模型时,更好地处理不确定性和进行概率推断。
2.2 分布列(PMF)
2.2.1 伯努利随机变量
伯努利随机变量是一种基本的离散随机变量,用于描述只有两种可能结果的单次实验,通常是“成功”或“失败”。例如,抛掷硬币的正面或反面,其中正面可能被编码为1(成功),反面为0(失败)。这种分布在评估任何二分案例中非常有用,如深度学习中的二分类问题。
2.2.2 二项随机变量
二项随机变量是对伯努利随机变量的扩展,表示固定次数的独立伯努利试验中成功的次数。参数 表示单次试验的成功概率。这适用于需要评估多次试验结果的场景,如在多次实验中模型正确分类的次数。
2.2.3 几何随机变量
几何随机变量度量在首次成功之前进行的试验次数。例如,连续抛硬币直到出现正面所需的次数。这种分布可以帮助分析需要多次尝试才能成功的过程,比如深度学习模型连续多次迭代直到达到某种性能标准。
# 下面是几何随机变量用plt画图的实现
import matplotlib.pyplot as plt
import numpy as np
# 设置成功概率
p = 0.3
# 生成k值从1到10
k = np.arange(1, 11)
# 计算几何分布的概率质量函数(PMF)
pmf = (1-p)**(k-1) * p
# 绘制几何分布的概率质量函数图
plt.figure(figsize=(8, 4))
plt.stem(k, pmf, basefmt=" ", use_line_collection=True)
plt.xlabel('Number of Trials')
plt.ylabel('Probability')
plt.title('Probability Mass Function of the Geometric Distribution')
plt.grid(True)
plt.show()
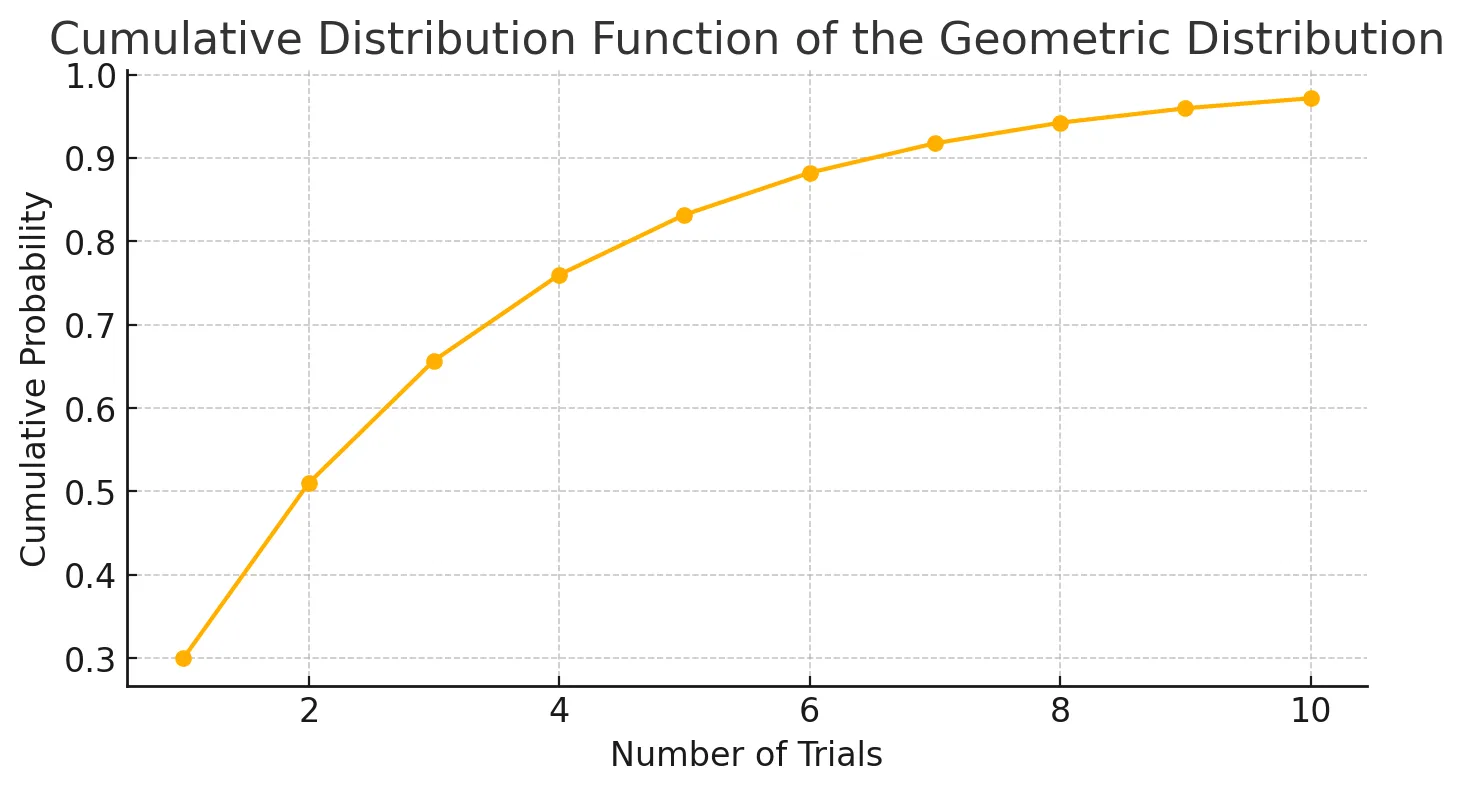
# 绘制几何分布的累积分布函数图
plt.figure(figsize=(8, 4))
plt.plot(k, cdf, marker='o')
plt.xlabel('Number of Trials')
plt.ylabel('Cumulative Probability')
plt.title('Cumulative Distribution Function of the Geometric Distribution')
plt.grid(True)
plt.show()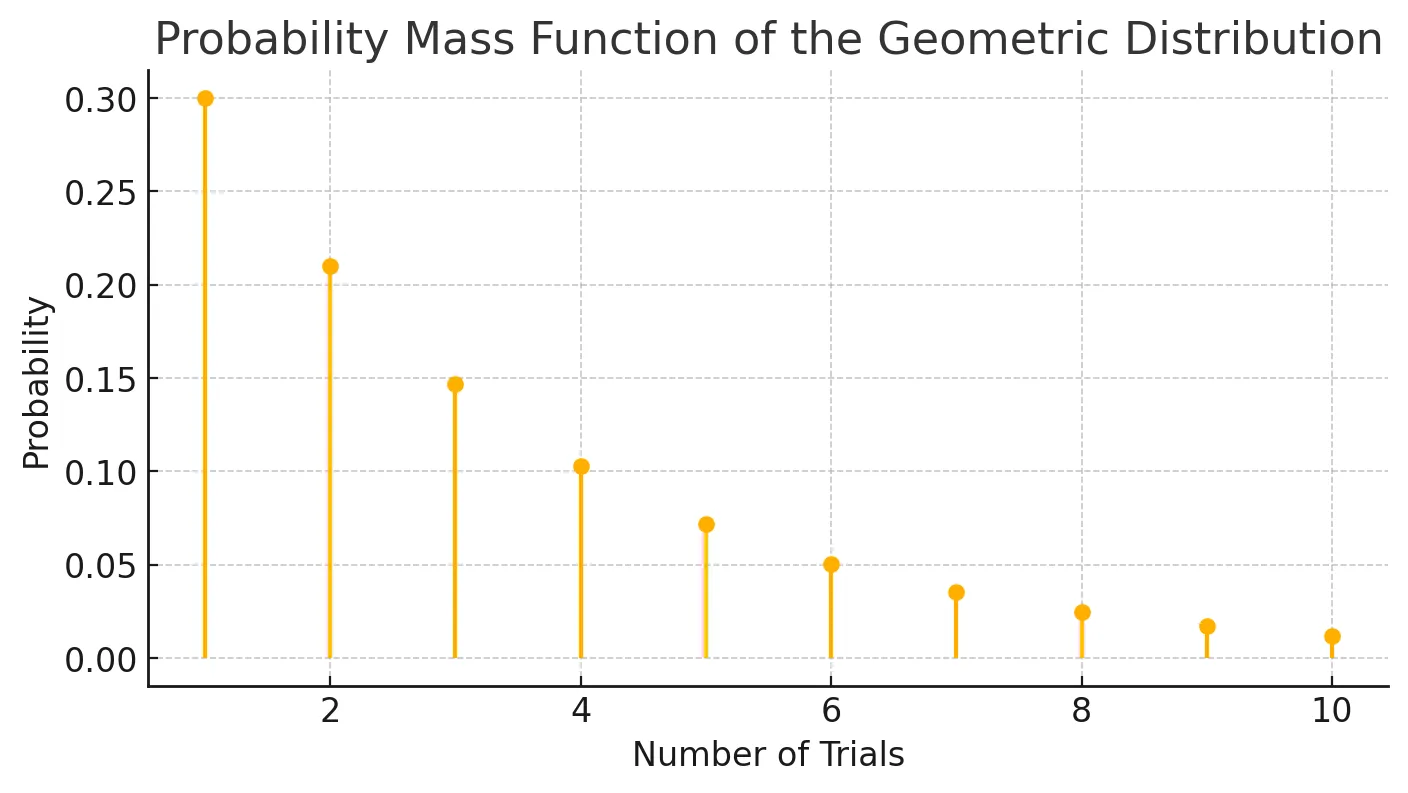
2.2.4 泊松随机变量
泊松随机变量用于描述在固定的时间间隔或空间区域内随机事件发生的次数。它非常适合于模拟稀有事件,如一段时间内接到的电话数量。在深度学习中,这可以用于模拟稀疏数据集中的事件分布,例如在自然语言处理中模拟单词的稀有使用情况。
# 下面是不努力和泊松用plt画图的实现
import numpy as np
import matplotlib.pyplot as plt
# 设定参数
p = 0.5 # 伯努利随机变量的概率
lambda_poisson = 3 # 泊松分布的λ值
# 伯努利分布
bernoulli_distribution = [1-p, p]
# 泊松分布,计算k=0到10的概率
poisson_distribution = [np.exp(-lambda_poisson) * lambda_poisson**k / np.math.factorial(k) for k in range(10)]
# 绘制图像
fig, axes = plt.subplots(1, 2, figsize=(14, 5))
# 伯努利分布图
axes[0].bar([0, 1], bernoulli_distribution, color=['blue', 'orange'])
axes[0].set_title('Bernoulli Distribution (p=0.5)')
axes[0].set_xticks([0, 1])
axes[0].set_xticklabels(['0', '1'])
axes[0].set_ylabel('Probability')
axes[0].set_xlabel('Value of Random Variable X')
# 泊松分布图
axes[1].bar(range(10), poisson_distribution, color='green')
axes[1].set_title('Poisson Distribution (λ=3)')
axes[1].set_xticks(range(10))
axes[1].set_xticklabels(range(10))
axes[1].set_ylabel('Probability')
axes[1].set_xlabel('Value of Random Variable X')
plt.tight_layout()
plt.show()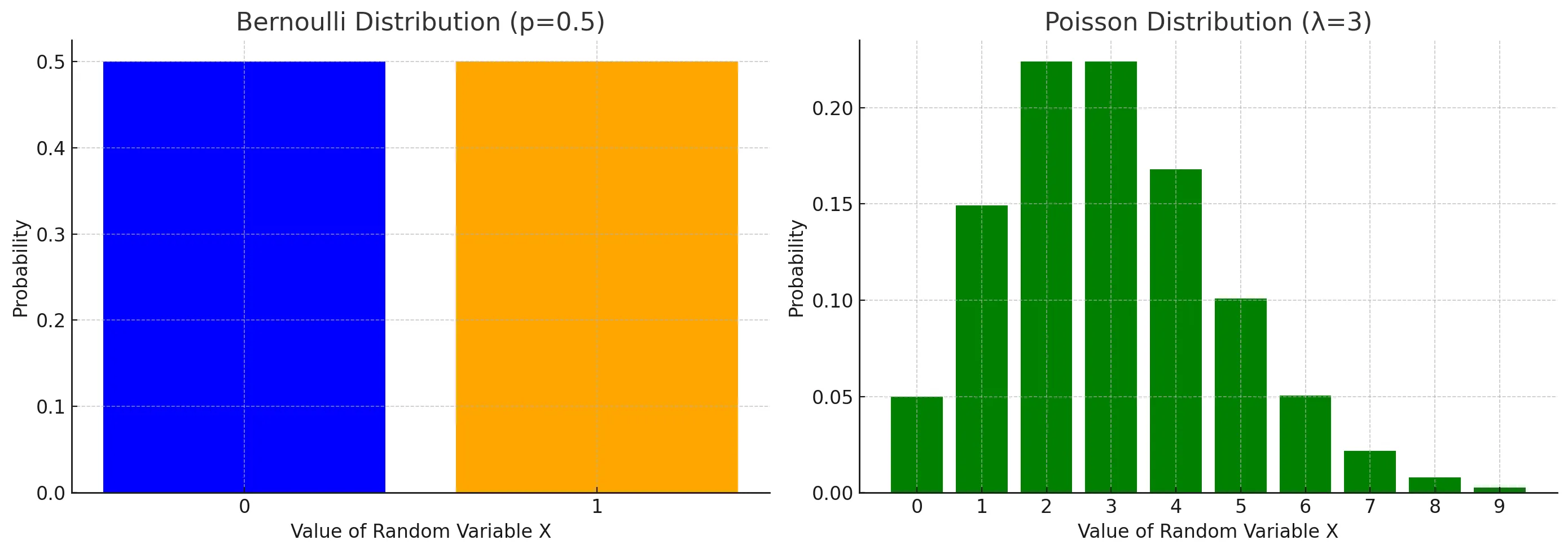
MIT概率论笔记第5节课离散随机变量
https://ruiboom.cn/posts/l5/