连续随机变量

2024-06-14

概率密度函数#

对于连续随机变量 $X$ ，存在函数 $f(x)$ ，满足对任意实数 $a \leq b$ ，有：

P(a \leq X \leq b) = \int_a^b f(x) \, dx

这里 $f(x) \geq 0$ ，并且积分的总和为1，即：

\int_{-\infty}^\infty f(x) \, dx = 1

多个连续随机变量#

联合概率密度函数#

当考虑两个连续随机变量 $X$ 和 $Y$ ，它们的联合概率密度函数 $f(x, y)$ 满足：

P((X, Y) \in A) = \int \int_A f(x, y) \, dx \, dy

这里 $f(x, y) \geq 0$ ，并且积分的总和也为1：

\int \int f(x, y) \, dx \, dy = 1

边缘概率密度函数#

从联合概率密度函数 $f(x, y)$ 中，可以导出 $X$ 和 $Y$ 的边缘概率密度函数：

f_X(x) = \int_{-\infty}^\infty f(x, y) \, dy

f_Y(y) = \int_{-\infty}^\infty f(x, y) \, dx

例题#

例题 1#

假设随机变量 $X$ 的概率密度函数为 $f(x) = 2x$ 在区间 $[0,1]$ 上。计算 $P(0.5 \leq X \leq 1)$ ：

P(0.5 \leq X \leq 1) = \int_{0.5}^1 2x \, dx = [x^2]_{0.5}^1 = 1 - 0.25 = 0.75

例题 2#

设 $X$ 和 $Y$ 为连续随机变量，其联合概率密度函数 $f(x, y) = 8xy$ 在区间 $x \in [0,1], y \in [0,1]$ 。求 $P(X < 0.5, Y < 0.5)$ ：

P(X < 0.5, Y < 0.5) = \int_0^{0.5} \int_0^{0.5} 8xy \, dy \, dx = [\int_0^{0.5} 4x^2y^2]_{0}^{0.5} = \frac{1}{16}

正态随机变量与高斯分布#

定义与公式#

高斯分布，也称为正态分布，是连续概率分布的一种。它在统计学、自然科学、社会科学、以及工程等领域中极为重要。高斯分布的概率密度函数（PDF）通常表示为：

f(x | \mu, \sigma^2) = \frac{1}{\sqrt{2\pi \sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}

其中：

$\mu$ 是均值，表示分布的中心，即平均值的位置。
$\sigma$ 是标准差，表示分布的宽度，其平方 $\sigma^2$ 称为方差。
$x$ 是变量。

性质#

对称性：正态分布是关于其均值对称的，这意味着在均值左右的行为是镜像对称的。
均值、中位数和众数的一致性：在正态分布中，这三个度量是相等的。
分布形状：标准差 $\sigma$ 决定了分布的扁平或尖峭程度。较小的 $\sigma$ 使得分布更尖锐，较大的 $\sigma$ 使分布更扁平。

下面是一个使用 Python 和 matplotlib 库来绘制不同参数（均值和方差）的正态分布图的例子。

import numpy as npimport matplotlib.pyplot as plt
# 定义正态分布的概率密度函数
def normal_distribution(x, mu, sigma):
    return (1 / (np.sqrt(2 * np.pi * sigma**2))) * np.exp(-((x - mu)**2) / (2 * sigma**2))
# 生成测试数据
x = np.linspace(-10, 10, 1000)
y1 = normal_distribution(x, 0, 1)  
y2 = normal_distribution(x, 0, 2)  
y3 = normal_distribution(x, -2, 1) 
# 画图
plt.figure(figsize=(10, 6))
plt.plot(x, y1, label='mu=0, sigma=1')
plt.plot(x, y2, label='mu=0, sigma=2')
plt.plot(x, y3, label='mu=-2, sigma=1')
plt.title('Normal Distribution')
plt.xlabel('X')
plt.ylabel('Probability Density')
plt.legend()
plt.grid(True)
plt.show()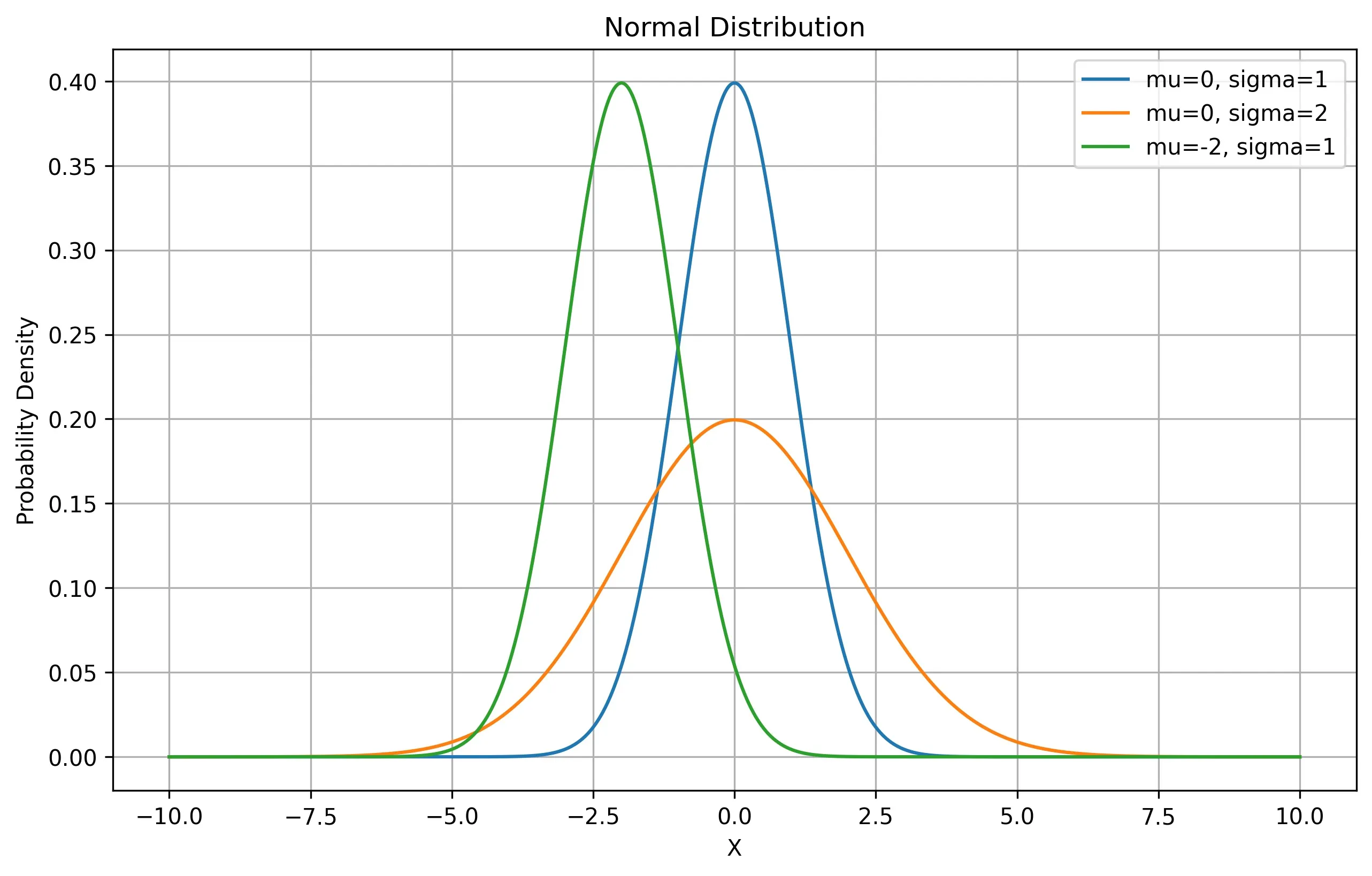

Local image

应用#

正态分布在实际应用中非常广泛，从自然现象的建模（如人类身高、测量误差等）到控制工程和风险管理中的财务分析等领域都有应用。正态分布的一个关键特性是中心极限定理，该定理指出，大量独立且同分布的随机变量之和趋近于正态分布，无论原始变量的分布如何。在深度学习里面，更多是以一个去噪的形象和身份来出现的。下面是它的应用。

图像数据去噪声#

在图像处理中，高斯滤波器常用于图像平滑，减少噪声。这种滤波器利用高斯函数的形状，对图像进行加权平均，有效地减轻图像的高频噪声。这是一种非常基础但强大的图像预处理步骤，可以改善后续深度学习模型的性能。

import cv2
import numpy as np
import matplotlib.pyplot as plt
image = cv2.imread('image.jpg')
image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB) 
# 应用高斯滤波
gaussian_blur = cv2.GaussianBlur(image, (5, 5), 0)
# 显示原图和处理后的图像
plt.figure(figsize=(10, 5))
plt.subplot(121), plt.imshow(image), plt.title('Original Image')
plt.subplot(122), plt.imshow(gaussian_blur), plt.title('Gaussian Blurred')
plt.show()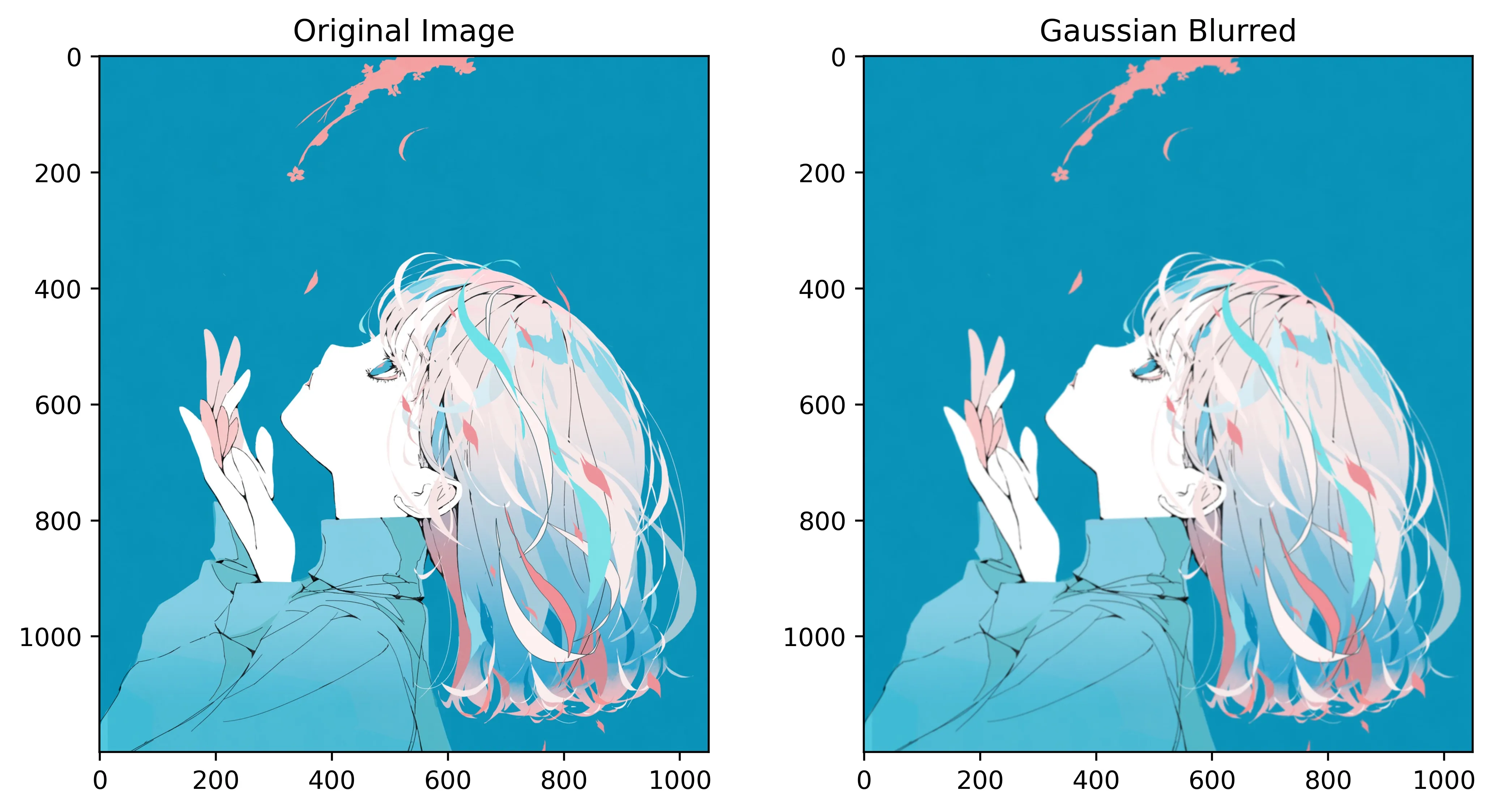

Local image

时间序列数据平滑#

在处理时间序列数据时，高斯分布常用于平滑数据，帮助去除短期波动，并突出显示趋势。这在金融市场分析、环境监测或任何类型的信号处理中尤其有用。

import numpy as np
import matplotlib.pyplot as plt
# 创建一些带有随机噪声的时间序列数据
t = np.linspace(0, 10, 100)
data = np.sin(t) + np.random.normal(scale=0.5, size=len(t))
# 高斯滤波平滑
smoothed_data = np.convolve(data, np.exp(-0.5 * (np.linspace(-2, 2, 30) ** 2)), mode='same')
# 绘制原始数据和平滑数据
plt.figure(figsize=(10, 5))
plt.plot(t, data, label='Original Data')
plt.plot(t, smoothed_data, color='red', label='Smoothed with Gaussian')
plt.legend()
plt.show()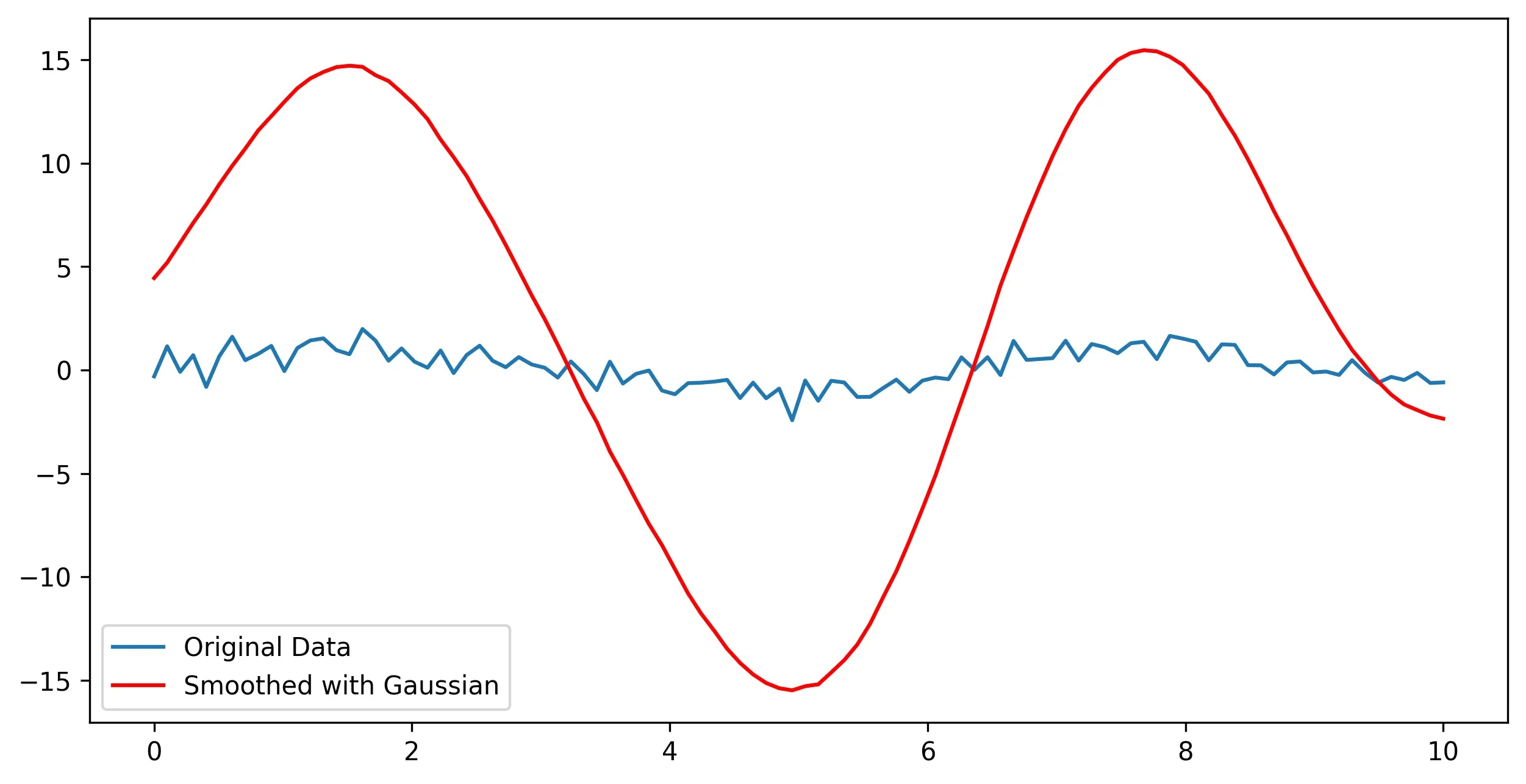

Local image

电磁数据分析#

在电磁数据分析中，如雷达信号或无线信号处理，高斯分布可用于建模背景噪声。这有助于在接收到的信号中识别出有意义的信号成分，从而提高检测的准确性。

import numpy as np
import matplotlib.pyplot as plt
# 模拟电磁信号
time = np.linspace(0, 1, 500)
signal = 2 * np.sin(2 * np.pi * 30 * time) + np.sin(2 * np.pi * 60 * time)
noise = np.random.normal(0, 0.5, len(time))
received_signal = signal + noise
# 绘制原始信号和带噪声的接收信号
plt.figure(figsize=(10, 5))
plt.plot(time, signal, label='Original Signal')
plt.plot(time, received_signal, label='Received Signal with Gaussian Noise')
plt.legend()
plt.show()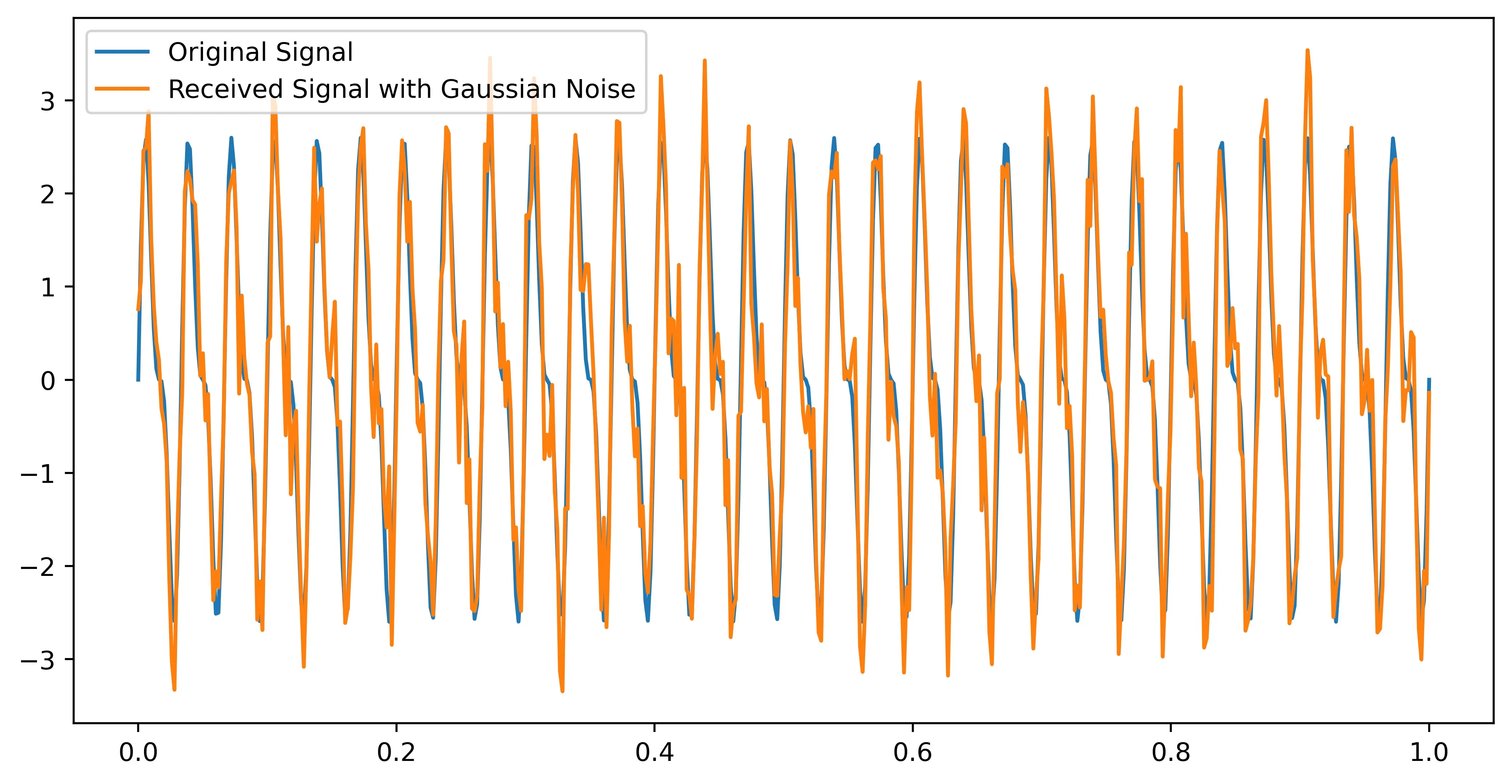

Local image

例题 3.1（年降雪量的概率）#

考虑一个地区的年降雪量 $X$ ，假设它服从均值为60英寸，标准差为20英寸的正态分布。计算该地区在一年内降雪量至少达到80英寸的概率：

P(X \geq 80) = 1 - \Phi\left(\frac{80 - 60}{20}\right) = 1 - \Phi(1) = 1 - 0.8413 = 0.1587

例题 3.2（信号处理中的误判概率）#

假设信号处理中的噪声 $N$ 是均值为0，标准差为1的正态分布。对于传输的信号 $S = -1$ ，若噪声 $N > 1$ ，接收端将错误地判断信号为 $S = 1$ 。该误判概率为：

P(N > 1) = 1 - \Phi(1) = 0.1587

多变量的联合概率密度#

在实际应用中，我们经常需要处理多个相关随机变量的情况。理解它们的联合分布是进行有效分析的关键。

例题 3.3（二维均匀分布）#

考虑罗密欧和朱丽叶的迟到时间 $X$ 和 $Y$ ，假设它们在区间 $[0,1]$ 内均匀独立地分布。因此，其联合概率密度函数为：

f_{X,Y}(x, y) = 1, \quad \text{for } 0 \leq x \leq 1 \text{ and } 0 \leq y \leq 1

此模型可以用于描述两个独立事件的随机性。

例题 3.4（平面上的均匀分布）#

设 $X$ 和 $Y$ 为单位正方形上的均匀随机变量，其联合概率密度函数为常数。因此，联合分布函数 $F_{X, Y}(x, y)$ 为：

F_{X, Y}(x, y) = xy, \quad \text{for } 0 \leq x, y \leq 1