1040 words
5 minutes
从世界坐标到相机坐标——相机标定和坐标系的变换
从相机拍摄到深度学习模型的数据处理流程
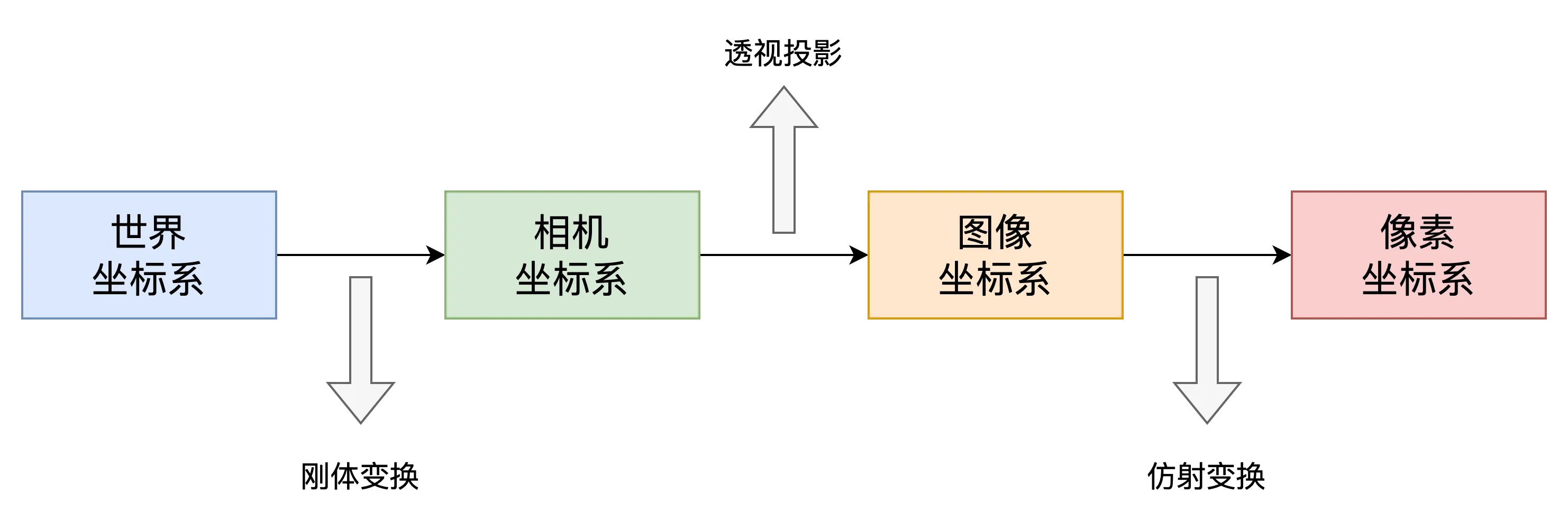
1. 世界坐标系
- 描述:真实世界中物体的三维坐标。
- 公式:不需要转换公式,直接作为参考。
2. 相机坐标系
- 描述:将物体的世界坐标转换为相对于相机位置和方向的坐标。
- 转换公式:
- 理解:R 是旋转矩阵,C 是相机在世界坐标系中的位置。
3. 图像坐标系
- 描述:通过相机镜头透视投影将三维的相机坐标转换为二维图像平面。
- 转换公式:
- 理解:f 是焦距,(X, Z) 是相机坐标系中的点。
4. 像素坐标系
- 描述:根据相机的内参,将图像坐标系中的点转换为实际图像的像素坐标。
- 转换公式:
- 理解:(p_x) 是像素尺度因子,(c_x) 是光学中心的x坐标。
5. 深度学习模型输入
- 描述:处理后的图像数据作为输入,用于训练或应用深度学习模型进行各种视觉任务。
几个坐标系直接的关系
通过一系列数学变换来实现:
世界坐标到相机坐标:
- 使用刚体变换(旋转和平移),以将世界坐标系中的点转换为相对于相机位置和方向的坐标。
- 公式:
- R 是旋转矩阵,C 是相机在世界坐标中的位置。
相机坐标到图像坐标:
- 通过相机的投影矩阵将三维相机坐标投影到二维图像平面上。
- 公式:
- f 是相机的焦距,X 和 Z 是相机坐标系中点的X和Z坐标。
图像坐标到像素坐标:
- 根据相机的内参矩阵,将图像坐标转换为最终的像素坐标。
- 公式:
- (p_x) 是每个像素的宽度,(c_x) 是图像中心的X坐标。
具体例子:从三维空间到像素坐标的转换
1. 从世界坐标到相机坐标的转换
- 步骤和计算:
- 使用旋转和平移,首先计算 :
- 旋转矩阵为单位矩阵,因此:
- 使用旋转和平移,首先计算 :
2. 从相机坐标到图像坐标的转换
- 应用透视投影公式:
- 同理:
3. 从图像坐标到像素坐标的转换
- 根据相机的内参矩阵转换:
- 假设像素尺度因子 像素/毫米,光学中心 :
- 假设像素尺度因子 像素/毫米,光学中心 :
通过这一系列步骤,我们将三维空间中的点转换成了图像上的一个像素点位置,该点位于像素坐标 (947.7, 633.8)。
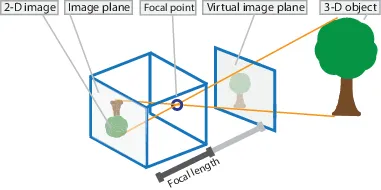
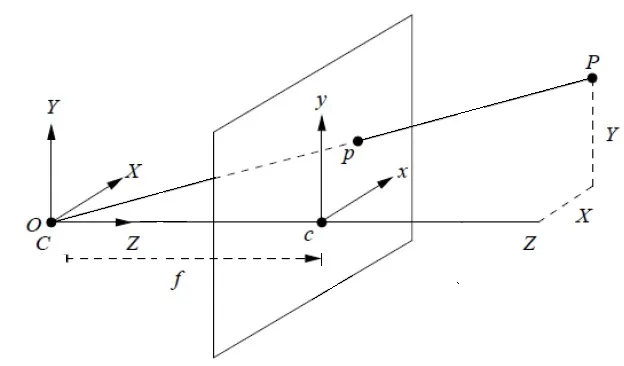
- C 是光心,可以想象为一个理想的单点透视源,代表镜头的中心。
- f 是焦距,即从光心 C 到成像平面的距离。成像平面在这里是与光心垂直的二维平面。
- 点 P 是三维空间中的一个点,其通过点 C 投射到成像平面上,形成了二维图像中的点 p。
Matlab相机标定工具箱获取内外参
为了确定相机的内参和外参,可以使用Matlab标定工具箱、Opencv图像处理库或者ROS中的相应标定包进行。
准备工作
- 棋盘格图片:准备相机标定专用的棋盘格图片,将其贴在一个平面上(标定平面)。
- 拍摄照片:使用待标定相机拍摄不同方向上的若干照片,一般以15张至20张为宜。

标定过程
- 角点提取:标定工具箱会自动提取出棋盘格的角点。
- 参数估计:进行相机内参、外参以及畸变参数的估计。
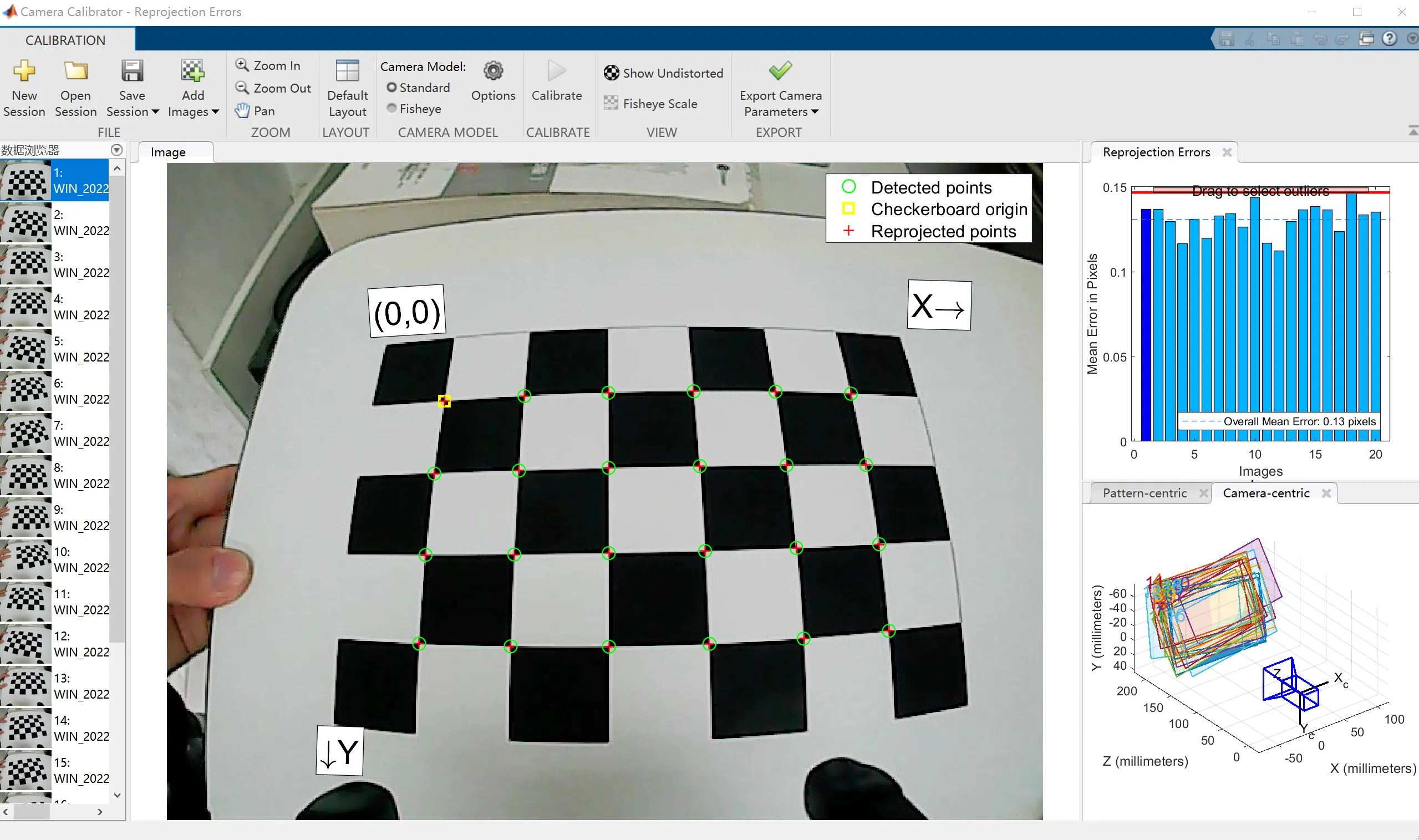
结果导出
- 导出参数:点击导出相机参数,能够获得相机的若干参数。
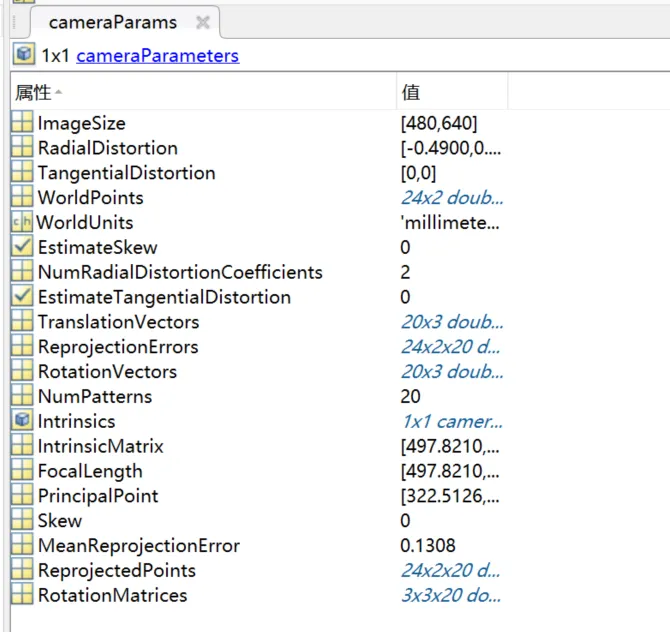
从世界坐标到相机坐标——相机标定和坐标系的变换
https://ruiboom.cn/posts/wtoc/